We recognize that academic language in primary school mathematics plays a decisive role in shaping learners’ conceptual understanding, problem-solving abilities, and long-term academic success. Mathematics is not only about numbers and operations; it is equally about language, structure, and meaning. When children struggle with mathematical language, they often struggle with mathematics itself. Therefore, addressing academic language early ensures equity, clarity, and confidence in mathematical learning.
In primary education, mathematical language introduces learners to precise terms, logical connectors, symbolic representations, and abstract reasoning. We focus on developing language-rich mathematics classrooms where students can interpret, articulate, and apply mathematical ideas accurately.
Understanding Academic Language in Mathematics
Academic language in mathematics refers to the specialized vocabulary, syntax, and discourse patterns used to communicate mathematical ideas. It includes:
-
Technical vocabulary (e.g., factor, quotient, estimate)
-
General academic words (e.g., analyze, compare, justify)
-
Symbolic language (e.g., +, −, =, >, <)
-
Sentence structures used in explanations and reasoning
We emphasize that academic language is cumulative. Each grade level builds on previously learned terms and structures, making early mastery essential for sustained achievement.
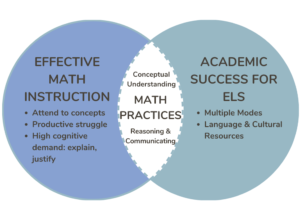
Why Academic Language Matters in Primary Mathematics
We observe that students who develop strong mathematical language skills demonstrate:
-
Improved problem comprehension
-
Clearer mathematical reasoning
-
Greater participation in discussions
-
Higher performance in assessments
Academic language enables learners to interpret word problems, understand instructions, and explain their thinking. Without explicit language instruction, mathematical concepts remain inaccessible to many learners, particularly multilingual students and those from language-limited environments.
Core Challenges in Tackling Mathematical Language
Vocabulary Density
Primary mathematics introduces a high volume of new terms in a short time. Words such as difference, table, or product have meanings in mathematics that differ from everyday usage, creating confusion.
Abstract Concepts
Mathematical language often represents abstract ideas that cannot be physically observed. Terms like value, relationship, and pattern require careful scaffolding.
Complex Sentence Structures
Word problems frequently use conditional phrases, comparatives, and logical connectors. These structures can overwhelm young learners if not explicitly taught.
Strategies for Building Academic Language in Mathematics
Explicit Vocabulary Instruction
We prioritize direct and intentional teaching of mathematical vocabulary. Each new term is introduced with:
-
Clear definitions
-
Visual representations
-
Contextual examples
-
Repeated exposure across lessons
By revisiting key terms consistently, we ensure that vocabulary becomes part of students’ active language.
Using Visual and Concrete Representations
We integrate manipulatives, diagrams, charts, and models to connect language with meaning. Visual support reduces cognitive load and allows learners to associate words with concepts. Number lines, arrays, fraction bars, and geometric models make academic language tangible.
Mathematical Talk and Classroom Discourse
We cultivate classrooms where structured mathematical talk is central to learning. Through guided discussions, students learn to:
-
Explain their reasoning
-
Justify solutions
-
Compare strategies
-
Use precise mathematical terms
Sentence starters such as “We noticed that…”, “The pattern shows…”, and “We can prove this by…” promote academic expression.
Integrating Reading and Writing in Mathematics
We embed reading and writing tasks within mathematics instruction to reinforce language development. These include:
-
Reading word problems aloud and silently
-
Writing explanations of solutions
-
Creating math journals
-
Summarizing strategies in complete sentences
Writing in mathematics clarifies thinking and strengthens conceptual understanding.
Scaffolding Language for Diverse Learners
Supporting Multilingual Learners
We implement targeted strategies to support multilingual students, including:
-
Pre-teaching key vocabulary
-
Using visuals and gestures
-
Encouraging use of first language for concept development
-
Gradually increasing language complexity
These approaches ensure that language barriers do not limit mathematical potential.
Differentiation Through Language Levels
We differentiate instruction by adjusting language demands while maintaining conceptual rigor. Tasks are designed with multiple entry points, allowing students to engage at varying levels of language proficiency without simplifying mathematical content.
Assessment of Academic Language in Mathematics
We assess not only correct answers but also language use in mathematical reasoning. Formative assessments include:
-
Oral explanations
-
Written justifications
-
Peer discussions
-
Performance-based tasks
By evaluating language alongside computation, we gain a holistic view of student understanding.
The Role of Teachers in Language-Rich Mathematics Instruction
We acknowledge that teachers are the primary facilitators of academic language. Effective practice includes:
-
Modeling precise mathematical language
-
Correcting misconceptions gently and clearly
-
Encouraging complete responses
-
Maintaining consistent terminology
Professional development focused on language-aware mathematics instruction enhances teaching quality and student outcomes.
Curriculum Design and Academic Language Alignment
We align curriculum materials with clear language progressions across grade levels. Well-designed curricula:
-
Introduce vocabulary systematically
-
Reinforce terms across units
-
Connect language to conceptual development
-
Provide opportunities for application
Consistency across grades prevents gaps and reinforces long-term mastery.
Family Engagement and Mathematical Language
We extend academic language beyond the classroom by engaging families. Providing parents with:
-
Vocabulary lists
-
Simple explanations of concepts
-
At-home discussion prompts
helps reinforce learning and builds a supportive environment for mathematical growth.
Long-Term Impact of Strong Mathematical Language Foundations
We recognize that early proficiency in mathematical academic language leads to:
-
Greater confidence in STEM subjects
-
Improved critical thinking skills
-
Enhanced academic literacy across disciplines
-
Stronger performance in higher-level mathematics
Primary school is the foundation upon which all future mathematical learning is built.
Conclusion: Advancing Mathematical Understanding Through Language
We affirm that tackling academic language in primary school mathematics is not an optional enhancement but a fundamental requirement for effective instruction. By embedding language development into every aspect of mathematics teaching, we empower learners to think, communicate, and succeed mathematically. Through explicit instruction, meaningful discourse, and consistent practice, we create inclusive classrooms where every child can access and master mathematical ideas with clarity and confidence.